牛客算法题

[TOC]

入门

简单

运行时间与排名成反比

NC3 链表中环的入口结点

题述

给一个长度为n链表，若其中包含环，请找出该链表的环的入口结点，否则，返回null。

数据范围： n -10000n≤10000，1<=结点值<=100001<=结点值<=10000

要求：空间复杂度 O(1)O(1)，时间复杂度 O(n)O(n)

例如，输入{1,2},{3,4,5}时，对应的环形链表如下图所示：

img

可以看到环的入口结点的结点值为3，所以返回结点值为3的结点。

解体思路

1. 这题我们可以采用双指针解法，一快一慢指针。快指针每次跑两个element，慢指针每次跑一个。如果存在一个圈，总有一天，快指针是能追上慢指针的。

2. 如下图所示，我们先找到快慢指针相遇的点，p。我们再假设，环的入口在点q，从头节点到点q距离为A，q p两点间距离为B，p q两点间距离为C。

3. 因为快指针是慢指针的两倍速，且他们在p点相遇，则我们可以得到等式 2(A+B)= A+ B + n(C+B)

4. 由3的等式，我们可得，C = A。(C有肯是转了好几个小圈子)

   • 论证：3等式化简得A=(n-1)(C+B)+C

   • 论证：慢指针转一圈内必然会和快指针相遇

5. 这时，因为我们的slow指针已经在p，我们可以新建一个另外的指针，slow2，让他从头节点开始走，每次只走下一个，原slow指针继续保持原来的走法，和slow2同样，每次只走下一个。

6. 我们期待着slow2和原slow指针的相遇，因为我们知道A=C，所以当他们相遇的点，一定是q了。

7. 我们返回slow2或者slow任意一个节点即可，因为此刻他们指向的是同一个节点，即环的起始点，q。

图片说明

public ListNode EntryNodeOfLoop(ListNode pHead)
	{
		ListNode slow = pHead;
		ListNode fast = pHead;
		do {
			if(fast.next==null||fast.next.next==null)
				return null;
			slow = slow.next;
			fast = fast.next.next;
		}while(slow!=fast);
    
		ListNode slow2 = pHead;	
		slow2 = pHead;		
    
		while(slow!=slow2){
			slow = slow.next;
			slow2 = slow2.next;
		};
		return slow;
	}

NC7 买卖股票的最好时机(一)

public int maxProfit (int[] prices) {
        // write code here
    	int max = 0;
    	int margin = 0;
    	int buyDay = 0;
    	for (int i = 0; i < prices.length; i++)
		{
    		margin = prices[i] - prices[buyDay];
    		if(margin>max) {
    			max = margin;
    		}
    		if(margin<0) {
    			buyDay = i;
    		}
		}
		return max;
    }

参考数据结构与算法分析java语言描述里的论述

大概思路

​ 设置margin，一旦margin大于max，就重置差值起点，继续寻找最大值；

NC9 二叉树中和为某一值的路径(一)

解法1:递归算法

/**
	 * 
	 * @param root TreeNode类
	 * @param sum  int整型
	 * @return bool布尔型
	 */
	static boolean flag = false;
	public boolean hasPathSum(TreeNode root, int sum)
	{
		
		// write code here
		if(root==null)
			return false;
		sum = sum - root.val;
		if(flag);
		if (root.left != null)
		{
			hasPathSum(root.left, sum);
		}
		if (root.right != null)
		{
			hasPathSum(root.right, sum);
		}
		if (root.left == null && root.right == null && sum == 0)
		{
			flag = true;
		}
		return flag;
	}

时间复杂度：O（N）：N是节点的个数

空间复杂度：O（H）：H是树的高度

---

NC11 将升序数组转化为平衡二叉搜索树

描述

给定一个升序排序的数组，将其转化为平衡二叉搜索树（BST）.

平衡二叉搜索树指树上每个节点 node 都满足左子树中所有节点的的值都小于 node 的值，右子树中所有节点的值都大于 node 的值，并且左右子树的节点数量之差不大于1

数据范围：0 \le n \le 100000≤n≤10000，数组中每个值满足 |val| \le 5000∣val∣≤5000 进阶：空间复杂度 O(n)O(n) ，时间复杂度 O(n)O(n)

例如当输入的升序数组为[-1,0,1,2]时，转化后的平衡二叉搜索树（BST）可以为{1,0,2,-1}，如下图所示：

img

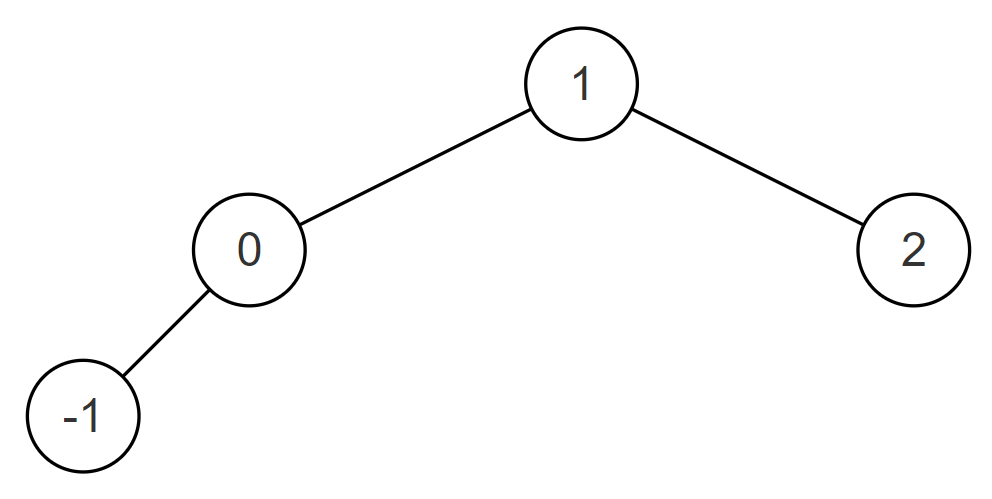
或为{0,-1,1,#,#,#,2}，如下图所示：

img

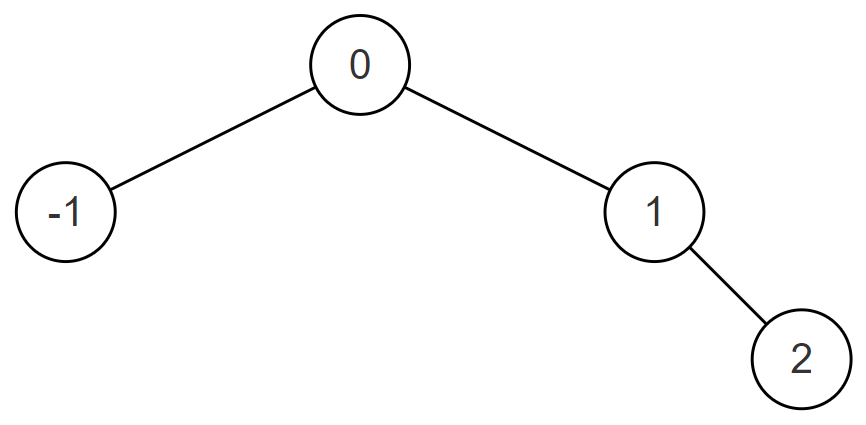
返回任意一种即可。

注意点：

1. 已经排序，所以使用二分法

2. 二分法除以二使用位运算更佳

3. 基准情形有限使用start>end

public TreeNode sortedArrayToBST(int[] num) {
    TreeNode root = sortedArrayToBST(num, 0, num.length-1);
    return root;

}


private TreeNode sortedArrayToBST(int[] num, int start, int end) {

    if (start > end) {
        return null;
    }
    int mid = (start + end) >> 1;
    TreeNode treeNode = new TreeNode(num[mid]);

    treeNode.left = sortedArrayToBST(num, start, mid - 1);
    treeNode.right = sortedArrayToBST(num, mid + 1, end);
    return treeNode;
}

NC16 对称的二叉树

描述

给定一棵二叉树，判断其是否是自身的镜像（即：是否对称） 例如： 下面这棵二叉树是对称的 下面这棵二叉树不对称。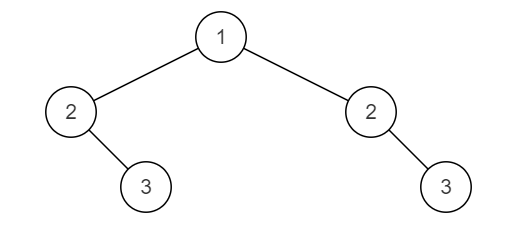

数据范围：节点数满足

0 \le n \le 10000≤n≤1000，节点上的值满足 |val| \le 1000∣val∣≤1000

要求：空间复杂度 O(n)O(n)，时间复杂度 O(n)O(n)

备注：

你可以用递归和迭代两种方法解决这个问题

错误思路

开始构想

1. 先进入最底层，从最底层开始判断是否平衡

2. 基准情形为全空，用bottom判断

存在的问题

1. 在不进入最低层时候就能判断出是否平衡

2. 失败的原因貌似是因为要去最后一层会生成指数倍的节点，出现溢出

private TreeNode emptyNode = new TreeNode(-1);

boolean isSymmetrical(TreeNode... nodes) {
    ArrayList<TreeNode> treeNodes = new ArrayList<>();
    boolean bottom = true;
    for (int i = 0; i < nodes.length; i++) {
        if (nodes[i] != null) {
            bottom = false;
        } else {
            nodes[i] = emptyNode;
        }
        treeNodes.add(nodes[i].left);
        treeNodes.add(nodes[i].right);
    }
    /**
         * 基准情形 全空
         */
    if (bottom) {
        return true;
    }
    boolean b = isSymmetrical(treeNodes.toArray(new TreeNode[treeNodes.size()]));
    //再判断是否对称
    int i = 0;
    int j = nodes.length - 1;
    while (i < j) {
        if (nodes[i] == emptyNode && nodes[j] == emptyNode) ;
        else if ((nodes[i] == emptyNode && nodes[j] != emptyNode) ||
                 (nodes[j] == emptyNode && nodes[i] != emptyNode))
            return false;
        else if (nodes[i].val != nodes[j].val) {
            return false;
        }
        i++;
        j--;
    }
    return true && b;

}

==正确思路==

方法一、递归：

如果一个树的左子树与右子树镜像对称，那么这个树是对称的。

img

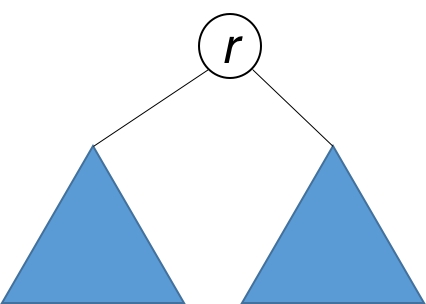
因此，该问题可以转化为：两个树在什么情况下互为镜像？

如果同时满足下面的条件，两个树互为镜像：

1. 它们的两个根结点具有相同的值。

2. 每个树的右子树都与另一个树的左子树镜像对称。

img

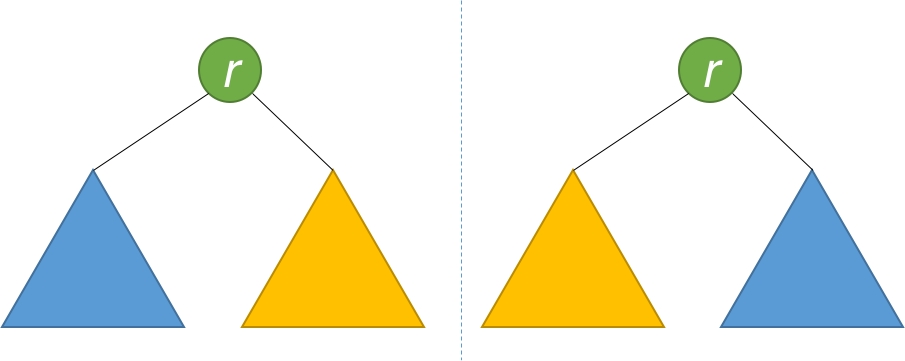
就像人站在镜子前审视自己那样。镜中的反射与现实中的人具有相同的头部，但反射的右臂对应于人的左臂，反之亦然。

顺藤摸瓜：

一次处理一对镜像节点，先处理内，后处理外

Java 代码实现

public boolean isSymmetric(TreeNode root) {
    return isMirror(root, root);
}

public boolean isMirror(TreeNode t1, TreeNode t2) {
    if (t1 == null && t2 == null) return true;
    if (t1 == null || t2 == null) return false;
    return (t1.val == t2.val)
        && isMirror(t1.right, t2.left)
        && isMirror(t1.left, t2.right);
}

方法二、迭代：

除了递归的方法外，我们也可以利用队列进行迭代。队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像。最初，队列中包含的是 root 以及 root。该算法的工作原理类似于 BFS，但存在一些关键差异。每次提取两个结点并比较它们的值。然后，将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。

Java 代码实现

public boolean isSymmetric(TreeNode root) {
    Queue<TreeNode> q = new LinkedList<>();
    q.add(root);
    q.add(root);
    while (!q.isEmpty()) {
        TreeNode t1 = q.poll();
        TreeNode t2 = q.poll();
        if (t1 == null && t2 == null) continue;
        if (t1 == null || t2 == null) return false;
        if (t1.val != t2.val) return false;
        q.add(t1.left);
        q.add(t2.right);
        q.add(t1.right);
        q.add(t2.left);
    }
    return true;
}

复杂度分析

• 时间复杂度：。因为我们遍历整个输入树一次，所以总的运行时间为 ，其中 是树中结点的总数。

• 空间复杂度：搜索队列需要额外的空间。在最糟糕的情况下，我们不得不向队列中插入 个结点。因此，空间复杂度为 。

NC19 连续子数组的最大和

题目描述

输入一个整型数组，数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为 O(n). 示例1 输入：[1,-2,3,10,-4,7,2,-5] 返回值：18 说明：输入的数组为{1,-2,3,10,—4,7,2,一5}，和最大的子数组为{3,10,一4,7,2}，因此输出为该子数组的和 18。

解题思路

**方法1：**连续的子数组，即数组中从i下标到j下标（0<=i<=j<数组长度）的数据，想要获得所有的子数组和，可以通过暴力法，两次循环获得，但时间复杂度为O(n^2)，效率不高。

**方法2：**动态规划，设动态规划列表 dp，dp[i] 代表以元素 array[i] 为结尾的连续子数组最大和。 状态转移方程： dp[i] = Math.max(dp[i-1]+array[i], array[i]); 具体思路如下： 1.遍历数组，比较 dp[i-1] + array[i] 和 array[i]的大小; 2.为了保证子数组的和最大，每次比较 sum 都取两者的最大值; 3.用max变量记录计算过程中产生的最大的连续和dp[i]；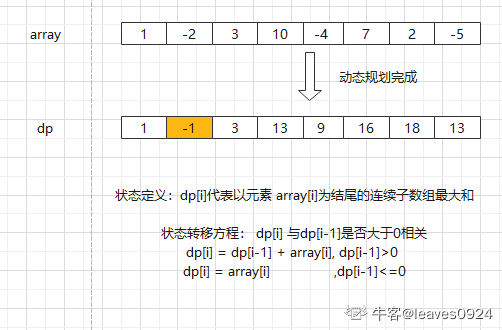

**方法3：**我们可以简化动态规划，使用一个变量sum来表示当前连续的子数组和，以及一个变量max来表示中间出现的最大的和。

代码实现

方法1：暴力法，时间复杂度O(n^2)，空间复杂度O(1)

方法2：动态规划，时间复杂度O(n)，空间复杂度O(n)

public int FindGreatestSumOfSubArray(int[] array) {
    int[] dp = new int[array.length];
    int max = array[0];
    dp[0] = array[0];
    for(int i=1;i<array.length;i++){
        // 动态规划，状态转移方程，确定dp[i]的最大值
        dp[i] = Math.max(dp[i-1] + array[i], array[i]);
        // 每次比较，保存出现的最大值
        max = Math.max(max,dp[i]);
    }
    return max;
}

==方法3：优化动态规划，时间复杂度O(n)，空间复杂度O(1)==!!!!

public int FindGreatestSumOfSubArray(int[] array) {
    int sum = 0;
    int max = array[0];
    for(int i=0;i<array.length;i++){
        // 优化动态规划，确定sum的最大值
        sum = Math.max(sum + array[i], array[i]);
        // 每次比较，保存出现的最大值
        max = Math.max(max,sum);
    }
    return max;
}

NC22 合并两个有序的数组

/*
* 最优解：从后往前处理,不需要开辟额外空间
*/
public void merge(int[] nums1, int m, int[] nums2, int n) {
    int i = m - 1, j = n - 1, index = m + n - 1;
    while (i >= 0 && j >= 0)
        nums1[index--] = nums1[i] > nums2[j] ? nums1[i--] : nums2[j--];
    while (j >= 0)
        nums1[index--] = nums2[j--];
}
//整洁！

注意对数组的访问尽可能避免越界

NC32 求平方根

我的思路

二分法，但是mid*mid会溢出，所以转换为long类型

public int sqrt2(int x)
{
    // write code here
    long longx = x;
    long left = 1;
    long right = x;
    long mid = (left + right) / 2;
    while (right - left > 1)
    {
        if (mid * mid == longx)
            left = right;
        else if (mid * mid > longx)
        {
            right = (left + right) / 2;
            mid = (left + right) / 2;

        } else
        {
            left = (left + right) / 2;
            mid = (left + right) / 2;
        }
    }
    return (int) mid;
}

改良二分法

public int sqrt1(int x)
{
    // write code here
    if(x<2)
    {
        return x;
    }
    int left = 0;
    int right = x;
    int mid = left + (right - left) / 2;
    int tempSqrt = x / mid;

    while (right-left>1)
    {

        if (mid == tempSqrt)
            return tempSqrt;
        else if (mid > tempSqrt)
        {
            right = mid;
            mid = left + (right - left) / 2;// 避免了溢出


        } else
        {
            left = mid;
            mid = left + (right - left) / 2;
        }
        tempSqrt = x / mid;
    }

    return left;
}

NC34 求路径

我的想法

动态规划题型

1	1	1
1	1+1=2	1+2=3
1	2+1=3	3+3=6

public int uniquePaths(int m, int n)
{
    // write code here

    int[][] paths = new int[m][n];
    Arrays.fill(paths[0], 1);

    for (int i = 0; i < paths.length; i++)
    {
        paths[i][0] = 1;
    }
    int i = 1;
    int j = 1;

    while (i != paths.length & j != paths[0].length)
    {
        while (j <= paths[0].length-1)
        {
            paths[i][j] = paths[i - 1][j] + paths[i][j - 1];
            j++;
        }
        j=i;
        i++;

        while (i <= paths.length-1)
        {
            paths[i][j] = paths[i - 1][j] + paths[i][j - 1];

            i++;
        }
        j++;
        i=j;
    }

    return paths[m - 1][n - 1];
}

NC61 两数之和 未学习完全

给出一个整型数组 numbers 和一个目标值 target，请在数组中找出两个加起来等于目标值的数的下标，返回的下标按升序排列。

（注：返回的数组下标从1开始算起，保证target一定可以由数组里面2个数字相加得到）

要求：空间复杂度 O(n)O(n)，时间复杂度 O(nlogn)O(nlogn)

我的想法

暴力算法，时间超时

public int[] twoSum (int[] numbers, int target) {
    // write code here
    int[] res =  new int[2];
    for (int i = 0; i < numbers.length; i++)
    {
        for (int j = i+1; j < numbers.length; j++)
        {
            if(numbers[i]-target==numbers[j]) {
                res[0]=i+1;
                res[1]=j+1;
                return res;
            }
        }
    }
    return res;
}

哈希算法

用空间换时间

public int[] twoSum (int[] numbers, int target) {
    // write code here
    HashMap<Integer, Integer> map = new HashMap<>();
    //遍历数组
    for (int i = 0; i < numbers.length; i++) {
        //将不包含target - numbers[i]，装入map中，包含的话直接返回下标
        if(map.containsKey(target - numbers[i]))
            return new int[]{map.get(target - numbers[i])+1, i+1};
        else
            map.put(numbers[i], i);
    }
    throw new IllegalArgumentException("No solution");
}

NC66 两个链表的第一个公共结点

我的想法

先遍历找到长短差，然后从同一位置开始找相同节点

public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2)
{
    int count1 = 0;
    int count2 = 0;
    ListNode p1 = pHead1;
    ListNode p2 = pHead2;
    boolean flag = true;
    if(p1==null||p2==null)return null;
    while (flag)
    {
        if (p1.next != null)
        {
            count1++;
            p1 = p1.next;
        }
        if (p2.next != null)
        {
            count2++;
            p2 = p2.next;
        }

        if (p1 == p2)
        {
            count1++;
            count2++;
            flag = false;
        } else if (p1.next == null && p2.next == null)
            return null;
    }
    p1 = pHead1;
    p2 = pHead2;
    if (count1 > count2)
    {
        for (int i = 0; i < count1 - count2; i++)
        {
            p1 = p1.next;
        }
    } else
    {
        for (int i = 0; i < count2 - count1; i++)
        {
            p2 = p2.next;
        }
    }
    while (p1 != p2)
    {
        p1=p1.next;
        p2=p2.next;
    }
    return p1;
}

其他思路

巧妙：交叉指针，一定会在某个点相遇，交点或者null

public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2)
{
    ListNode p1 = pHead1;
    ListNode p2 = pHead2;
    if(p1==null||p2==null)
        return null;
    while(p1!=p2)
    {
        p1=p1.next;
        p2=p2.next;
        if(p1 != p2){
            if(p1 == null)p1 = pHead2;
            if(p2 == null)p2 = pHead1;
        }
    }
    //有交集的链不会指向null，因为此时已经相等
    //若无交集会在null时相等，相当于相交链是空链
    return p1;
}

NC69 链表中倒数最后k个结点

• 输入一个长度为 n 的链表，设链表中的元素的值为 ai ，返回该链表中倒数第k个节点。

• 如果该链表长度小于k，请返回一个长度为 0 的链表。

• 要求：空间复杂度 O(n)O(n)，时间复杂度 O(n)O(n)

• 进阶：空间复杂度 O(1)O(1)，时间复杂度 O(n)O(n)

我的思路

使用数组记录

时间复杂度O(n),空间复杂度O(n)

public ListNode FindKthToTail (ListNode pHead, int k) {
    // write code here
    ArrayList<ListNode> nodeArray = new ArrayList<ListNode>();
    ListNode p = pHead;
    while(p!=null)
    {
        nodeArray.add(p);
        p=p.next;
    }
    if(k>nodeArray.size()||k==0)return null;
    return nodeArray.get(nodeArray.size()-k);
}

其他思路

双指针，第一个与第二个间隔k，第一个到尾部，第二个位置便是最后k个节点

public ListNode FindKthToTail (ListNode pHead, int k)
{
    ListNode p1 = pHead;
    ListNode p2 = pHead;
    for (int i = 0; i < k; i++)
    {
        if(p1==null)return null;
        p1=p1.next;
    }
    while(p1!=null)
    {
        p1=p1.next;
        p2=p2.next;
    }
    return p2;
}

NC70 单链表的排序

使用冒泡算法，两两交换，理论很简单，但链表实现起来有些难度

可优化的点：控制什么时候结束

public ListNode sortInList(ListNode head)
{
    // write code here
    ListNode fake = new ListNode(0);
    fake.next = head;
    ListNode pre = fake;
    ListNode p = pre.next;
    ListNode q = p.next;
    ListNode t = fake.next;
    int length = 0;
    // 先遍历寻找长度
    while(t!=null)
    {
        length++;
        t=t.next;
    }
    for(int i=0;i<length;i++)
    {
        while (q != null)
        {
            if (p.val > q.val)
            {
                swap(pre);
                pre = q;
                q = p.next;
            }else
            {
                pre=pre.next;
                p = pre.next;
                q = p.next;
            }

        }

        pre = fake;
        p = pre.next;
        q = p.next;
    }
    return fake.next;

}

private void swap(ListNode pre)
{
    ListNode p = pre.next;
    ListNode q = p.next;
    p.next = q.next;
    q.next = p;
    pre.next = q;
}

NC192 二叉树的后序遍历

非递归算法--两个栈

思路： 这是一个非常巧妙的算法，后序遍历的顺序为左、右、根，反过来就是根、右、左，类似先序遍历的根、左、右， 先序遍历的非递归很简单：根节点入栈，出栈并依次判断右、左子树，有右入右，有左入左，然后循环出栈判断，后续遍历的反向遍历就是在 出栈判断时，先入左，后入右

import java.util.*;
public class Solution {
    public int[] postorderTraversal (TreeNode root) {
        // write code here
        if(root==null)return new int[0];
      
        Stack<TreeNode> s1=new Stack<>();
        Stack<TreeNode> s2=new Stack<>();
      
        TreeNode p=root;
        s1.push(p);

        while(!s1.empty()){
            p=s1.pop();
            s2.push(p);
            if(p.left!=null)s1.push(p.left);
            if(p.right!=null)s1.push(p.right);
        }
        
        int[] res=new int[s2.size()];
        for(int i=0;i<res.length;i++){
            res[i]=s2.pop().val;
        }
        return res;
    }
}

非递归算法-一个栈

import java.util.*;
public class Solution {
    public int[] postorderTraversal (TreeNode root) {
        // write code here
        if(root==null)return new int[0];
        
        Stack<TreeNode> s=new Stack<>();
        List<Integer> list=new ArrayList<>();
        //定义两个指针，t指向栈顶，c指向刚出栈的节点,初始都指向root
        TreeNode t=root;
        TreeNode c=root;
        s.push(t);
      
        //进入循环，判断条件栈不为空
        while(!s.empty()){
            //t赋值为栈顶元素
            t=s.peek();
            //判断左子树是否为空，以及上一个弹出节点是否为左子树，以及是否为右子树
            if(t.left!=null&&c!=t.left&&c!=t.right){
                s.push(t.left);
            //判断右子树是否为空，以及上一个弹出节点是否为右子树
            }else if(t.right!=null&&c!=t.right){
                s.push(t.right);
            //弹出该节点，然后指针指向该弹出节点
            }else{
                list.add(t.val);
                s.pop();
                c=t;
            }
        }
        
        int[] res=new int[list.size()];
        for(int i=0;i<res.length;i++){
            res[i]=list.get(i);
        }
        return res;
    }
}

PS:只记录需要记录的